[ history
| architecture
| stratodesic
| kits
| links
| vrml
| trademark
]


Geodesic and
Stratodesic(tm)
Domes
Domes: The Engineering Wonder
- Domes maximize volume while minimizing surface area...
- providing structural integrity with a minimum of energy/material
- making them perfectly stable and inert as molecular packages.
- They are energy efficient as architectural structures - retaining heat, while minimizing solar heat load
- and they minimize drag and distribute wind/snow loads
- ... and they're just durn pretty to look at!
History
Many cultures have developed complex, spheroidal polyhedra for use in woven bowls, hats and even structures.
However, the Greeks were first to record mathematical models of geodesic forms - they created a plethora of regular
polyhedra: tetrahedrons, cubes, icosohedrons, dodecahedrons, etc. It was the Romans who first used geometric
framing to build concrete domes, introducing the dome as a common architectural element which has survived in modern
forms today.
In the 1920's, a German scientist/engineer, Walter Bauersfeld, created the first metal-reinforced, concrete
geodesic dome. It was designed to house the first planetarium, created by Zeiss Optical Works in Jena, Germany.
In the 1940's Buckminster Fuller adopted the Greek's icosohedron to produce his
Dymaxion or Geodesic Dome for use in architectural structures. Using his icosohedral
dome as the basis for a cartographic projection, Fuller became the only person to have been awarded
a patent for a map-making process (today, we might call it a texture-mapping algorithm...).
Recent discoveries of complex, but highly stable, polyhedral molecules have been called Buckminster-Fullerines
and Bucky-balls in his honor.
While Fuller's work on Geodesic Domes produced quite a bit of excitement among many young engineers --
particularly during the '60s Earth movement -- the geodesic dome fell far short of the expectations that
many had placed on it: the economical solution to efficient homebuilding.
There are several reasons for this shortfall:
- Icosohedral domes contain few horizontal and vertical planes,
necessary for conventional architectural framing.
- Specially cut and assembled parts increases construction costs.
- Non-conventional framing makes it harder to acquire a building permit.
- Ill-planned doors and windows often degrade structure integrity and energy efficiency.
- Conventional furnishings and fixtures rarely fit well in curved spaces, reducing spatial efficiency.
- Dome-shaped buildings are not often well-received by suburban architectural review committees.
- Use of modern insulation reduces the cost-benefit of domes over conventional construction.
- Some of the early dome "cabin" constructions were just simply ugly.
Having said that, there are many beautiful dome homes built around the world, and a large,
enthusiastic crowd of dome supporters. With the growth of the Internet, a recent resurgence in dome interest has taken hold --
and many people are beginning to rediscover domes as a fun, structurally secure and ecologically-minded form for homes.

An Architecturally Sensible Dome
I have been interested in geodesic domes since the early 70's, and began writing software programs for
creating dome parts-lists while in high school.
The photo on the right shows a 25 foot diameter dome I convinced the school to sponsor -
I calculated the number and length of studs, created a jig in shop for pressing and drilling the ends,
and on the day that we assembled it -- lo and behold, it actually worked!
During the process of completing that project, it became quickly obvious that icosohedral domes just weren't
the optimal shape for most architectural applications. So I started experimenting with dodecahedral-based domes
and other geometries.
During my freshman year (1975) at Cal Poly (an architectural school in central California) I entered the
annual Poly Royal architectural contest. These were the parameters:
Design and build a temporary structure that could be carried into Poly Canyon (behind the campus), assemble it,
spend the weekend in it and take it back down with low environmental impact. It had to be
stable/warm/dry enough to house all the people who carried it up there.
 The photo on the right is of my group taking our project down after having won 1st place in the
state-wide contest.
I had used a pad of paper to come up with the polyhedral shape (Rhombicosidodecahedron), and a hand-held
HP calculator to determine panel sizes.
The photo on the right is of my group taking our project down after having won 1st place in the
state-wide contest.
I had used a pad of paper to come up with the polyhedral shape (Rhombicosidodecahedron), and a hand-held
HP calculator to determine panel sizes.
My design was cited for several reasons:
- Least expensive: it cost $2 for the staples - the surface was recycled, water-repellent cardboard.
Other teams had spent up to $250 on materials.
- No environmental impact
- Energy efficient - our body heat kept the space toasty at night; 5 removable window panels regulated temperature.
- Strong - it was the only structure that would take the weight of 2 students on top.
- Easy to transport - see photo. We had carried it up as a stack of panels and assembled it --
when the contest was over, we just carried it down whole. Low weight and
wind resistance made this easy to accomplish.
This dome turned out to have fairly unique, and useful, properties: all the dome panels were identical squares,
equilateral triangles and regular pentagons.
I had segmented the pentagons into isosceles triangles to
reduce transportation size, increase structural strength and minimize construction waste.
This provided several advantages:
- The panels were simple and material-efficient to create.
- Interchangeable panels made assembly fast and easy.
- A vertical door could be cut into the structure without compromising
the integrity of the structure.
 However, even this dome was not perfect for architectural applications. After Cal Poly,
I went to work for SysComp/Data General, creating 3D modeling and rendering systems. The photo on the right
was shot directly off of a Tektronix monitor (c. 1982), using another dome generating utility I wrote.
However, even this dome was not perfect for architectural applications. After Cal Poly,
I went to work for SysComp/Data General, creating 3D modeling and rendering systems. The photo on the right
was shot directly off of a Tektronix monitor (c. 1982), using another dome generating utility I wrote.
Soon afterwards, it occurred to me to take another approach to doing architectural domes - why make them geodesic,
at all? I had just completed a program that triangulated 3D contour models, and decided to apply that to spherical shapes.
The domes below use the Stratodesic(tm) algorithm I came up with.
The key feature to this dome is that you can easily deform the spherical shape into ellipsoids and
other spheroidal shapes without compromising structural integrity.
A secondary feature is that it is made up of a series of horizontal slices and a number of vertical planes.
This makes it ideal for architectural applications, in that you can change its proportions and cut the dome horizontally at just about
any spot and still maintain its structural integrity -- plus beam/stud sizes are regular; and door/window jams can line up --
unlike that in geodesic domes. This supports architectural applications that are energy efficient, structurally
sound and water-tight.
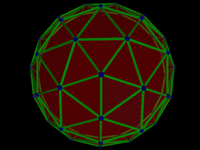
Geodesic vs Stratodesic
A dome is any object with a shell-like spheroid shape.
Typically, domes are truncated, so that they can sit on a surface, such as the ground.
Domes can be grouped into a number of categories: non-geometric, polyhedral, geodesic and stratodesic.
Geometric domes have some underlying, symmetrical structure; non-geometric domes include solid shells such as ceramic bowls.
Polyhedral domes are geometrics made up of interconnecting facets; geodesic domes are polyhedral domes with a
regular polygonal structure.
Dymaxion was coined by Buckminster Fuller to describe his set of geodesic domes -- typically icosohedrally based.
Stratodesic domes were coined by me in early 1996 to describe domes I had been creating since the early 1980's.
While stratodesic domes are polyhedral, they are not geodesic. Whereas geodesic domes are based on radial symmetry,
stratodesic domes are based on axial symmetry.
Geodesic domes are optimally stable when loads are directed at it from all directions;
stratodesic domes are optimally stable when the primary load is along it's axis.
This makes stratodesic domes better suited for most architectural applications.
 Geodesic domes tend to form Great Circles that split the dome into hemispheres, with few (if any) parallel planes --
making it difficult to use conventional framing methods without degrading structural integrity.
Since stratodesic domes are axially symmetrical, they form numerous parallel planes -- ideal for foundations, beams, joists and headers.
Geodesic domes tend to form Great Circles that split the dome into hemispheres, with few (if any) parallel planes --
making it difficult to use conventional framing methods without degrading structural integrity.
Since stratodesic domes are axially symmetrical, they form numerous parallel planes -- ideal for foundations, beams, joists and headers.
While geodesic domes are the best choice for many non-architectural applications, the optimal architectural choice will typically be Stratodesic(tm).
Building a Statodesic(tm) Dome
I will be provided a web form in the future that will allow you to generate a parts list for building your own
Stratodesic domes. I hope to also provide a kit that will assist in building Stratodesic domes.
Other Dome References
 Michael Rader's dome resource page
Michael Rader's dome resource page
 Kirby Urner's primer on dome geometry
Kirby Urner's primer on dome geometry
 Kirby Urner's table of dome manufacturers
Kirby Urner's table of dome manufacturers
 The Buckminster Fuller Institute
The Buckminster Fuller Institute
 Kenneth Snelson' Tensegrity Page
Kenneth Snelson' Tensegrity Page
 Jack and Linda Lydick's dome architecture
Jack and Linda Lydick's dome architecture
VRML and VR Modeling
If you are interested in 3D rendering, check out VR World
for info and demos on VRML Modeling.
Virtual Reality Modeling Language is the Internet standard for modeling, rendering and navigating through 3D space.
Whereas HTML provides a 2D standard for rending text, images and links, VRML provides a real-time mechanism for manipulating 3D models and
providing web links in a 3D context.
If you have a VRML browser installed, give my
VRML Dome Generator a try.



The above examples are all stratodesic domes, and were generated via VRML using a short PERL script.
The wireframe egg was rendered using Netscape's VRML browser
The Easter Egg, a texture-mapped version of the egg dome, was rendered using Chaco's VRML browser.
The Red Dome was generated using my VRML Dome Generator.
The name Stratodesic(tm) is a trademark of Robert M. Free
For more information on this web page, email domes@graphcomp.com.
 However, even this dome was not perfect for architectural applications. After Cal Poly,
I went to work for SysComp/Data General, creating 3D modeling and rendering systems. The photo on the right
was shot directly off of a Tektronix monitor (c. 1982), using another dome generating utility I wrote.
However, even this dome was not perfect for architectural applications. After Cal Poly,
I went to work for SysComp/Data General, creating 3D modeling and rendering systems. The photo on the right
was shot directly off of a Tektronix monitor (c. 1982), using another dome generating utility I wrote.


 The photo on the right is of my group taking our project down after having won 1st place in the
state-wide contest.
I had used a pad of paper to come up with the polyhedral shape (Rhombicosidodecahedron), and a hand-held
HP calculator to determine panel sizes.
The photo on the right is of my group taking our project down after having won 1st place in the
state-wide contest.
I had used a pad of paper to come up with the polyhedral shape (Rhombicosidodecahedron), and a hand-held
HP calculator to determine panel sizes.

 Geodesic domes tend to form Great Circles that split the dome into hemispheres, with few (if any) parallel planes --
making it difficult to use conventional framing methods without degrading structural integrity.
Since stratodesic domes are axially symmetrical, they form numerous parallel planes -- ideal for foundations, beams, joists and headers.
Geodesic domes tend to form Great Circles that split the dome into hemispheres, with few (if any) parallel planes --
making it difficult to use conventional framing methods without degrading structural integrity.
Since stratodesic domes are axially symmetrical, they form numerous parallel planes -- ideal for foundations, beams, joists and headers.

